Kamis, 19 Mei 2022

SOAL ATURAN SIN DAN ATURAN COS


Jawab:

1. Berdasarkan aturan sinus pada perbandingan sisi-sisi segitiga maka diperoleh perhitungan berikut!

table attributes columnalign right center left columnspacing 0px end attributes row cell fraction numerator sin space 45 degree over denominator AC end fraction end cell equals cell fraction numerator sin space 60 degree over denominator AB end fraction end cell row cell fraction numerator begin display style 1 half end style square root of 2 over denominator AC end fraction end cell equals cell fraction numerator begin display style 1 half end style square root of 3 over denominator 12 end fraction end cell row cell 12 cross times 1 half square root of 2 end cell equals cell 1 half square root of 3 AC end cell row cell 12 square root of 2 end cell equals cell square root of 3 AC end cell row AC equals cell fraction numerator 12 square root of 2 over denominator square root of 3 end fraction end cell end table 

Kemudian sederhanakan bentuk akar diatas dengan mengalikannya dengan sekawan.

table attributes columnalign right center left columnspacing 0px end attributes row AC equals cell fraction numerator 12 square root of 2 over denominator square root of 3 end fraction cross times fraction numerator square root of 3 over denominator square root of 3 end fraction end cell row blank equals cell fraction numerator 12 square root of 6 over denominator 3 end fraction end cell row blank equals cell 4 square root of 6 end cell end table

Dengan demikian, panjang sisi AC adalah 4 square root of 6 space cm.


2.

Besar sudut A = 180 ° – (B +C) , sehingga sudut a sebesar 85 °

Jadi, besarnya sudut kemiringan Menara Pisa yaitu x = 90 ° – 85 ° = 5 °.

3. 


4. 



5. Dengan menggunakan aturan sinus perbandingan panjang sisi segitiga, diperoleh 

table attributes columnalign right center left columnspacing 0px end attributes row cell fraction numerator straight a over denominator sin space straight A end fraction end cell equals cell fraction numerator straight c over denominator sin space straight C end fraction end cell row cell fraction numerator straight a over denominator sin space 30 degree end fraction end cell equals cell fraction numerator straight b over denominator sin space open parentheses 180 degree minus 30 degree minus 60 degree close parentheses end fraction end cell row cell fraction numerator straight a over denominator sin space 30 degree end fraction end cell equals cell fraction numerator straight c over denominator sin space 90 degree end fraction end cell row cell fraction numerator straight a over denominator begin display style 1 half end style end fraction end cell equals cell straight c over 1 end cell row cell 2 straight a end cell equals straight c row straight c equals cell 2 straight a end cell end table 

Karena straight a plus straight c equals 9 space cm, maka 

table attributes columnalign right center left columnspacing 0px end attributes row cell straight a plus straight c end cell equals 9 row cell straight a plus 2 straight a end cell equals 9 row cell 3 straight a end cell equals 9 row straight a equals cell 3 space cm end cell row blank blank blank row straight c equals cell 2 straight a end cell row blank equals cell 2 times 3 end cell row blank equals cell 6 space cm end cell end table 

Selanjutnya dengan menggunakan aturan cosinus perbandingan panjang sisi segitiga, diperoleh 

table attributes columnalign right center left columnspacing 0px end attributes row straight b equals cell square root of straight a squared plus straight b squared minus 2 times straight a times straight b times cos space straight B end root end cell row blank equals cell square root of 3 squared plus 6 squared minus 2 times 3 times 6 times cos space 60 degree end root end cell row blank equals cell square root of 9 plus 36 minus 2 times 3 times 6 times 1 half end root end cell row blank equals cell square root of 9 plus 36 minus 18 end root end cell row blank equals cell square root of 27 end cell row blank equals cell 3 square root of 3 space cm end cell end table 

Jadi, panjang sisi straight b adalah 3 square root of 3 space cm. 


6. b = 2 cm
c = 3 cm
< A = 60°
a = ....???

a^2 = b^2 + c^2 - 2bc cos A
a^2 = 2^2 + 3^2 - 2(2)(3) cos 60°
a^2 = 4 + 9 -12(1/2)
a^2 = 13 - 6
a^2 = 7
a = \/7 (akar 7)

7. 
















8. 













9. luas ∆ = 1/2 × AC × BC × sin C


10. 
AC² = BC² + AB² - 2 . BC . AB cos B
AC² = 60² + 30² - 2 . 60 . 30 cos 120°
AC² = 3600 + 900 - 2 . 1800 (-1/2)
AC² = 3600 + 900 + 1800
AC² = 6300
AC = √6300
AC = √900 . √7
AC = 30 √7

Jadi jarak kapal dari tempat pemberangkatan (awal) ke pemberhentian (akhir) adalah
30 √7 km




Jawab:
1. Gambar segitiga ABC:

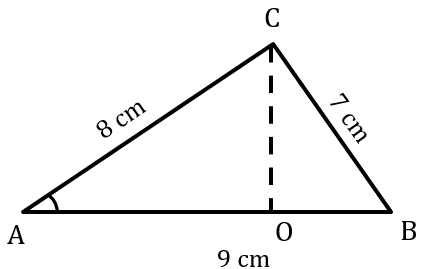
Menghitung nilai cos pada sudut A dengan menggunakan aturan cosinus:

begin mathsize 14px style table attributes columnalign right center left columnspacing 0px end attributes row blank blank cos end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank space end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank straight A end table table attributes columnalign right center left columnspacing 0px end attributes row blank equals blank end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank cell fraction numerator AC squared plus AB squared minus BC squared over denominator 2 times AC times AB end fraction end cell end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank cos end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank space end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank straight A end table table attributes columnalign right center left columnspacing 0px end attributes row blank equals blank end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank cell fraction numerator 8 squared plus 9 squared minus 7 squared over denominator 2 times 8 times 9 end fraction end cell end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank cos end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank space end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank straight A end table table attributes columnalign right center left columnspacing 0px end attributes row blank equals blank end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank cell fraction numerator 64 plus 81 minus 49 over denominator 144 end fraction end cell end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank cos end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank space end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank straight A end table table attributes columnalign right center left columnspacing 0px end attributes row blank equals blank end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank cell 96 over 144 end cell end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank cos end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank space end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank straight A end table table attributes columnalign right center left columnspacing 0px end attributes row blank equals blank end table table attributes columnalign right center left columnspacing 0px end attributes row cell 2 over 3 end cell equals cell AO over AC end cell end table end style

Menghitung panjang sisi segitiga siku-siku:
a) Panjang AO:

begin mathsize 14px style table attributes columnalign right center left columnspacing 0px end attributes row AO equals cell 2 over 3 cross times text AC end text end cell row blank equals cell 2 over 3 cross times 8 space text cm end text end cell row blank equals cell 16 over 3 space text cm end text end cell end table end style

b) Panjang CO:

begin mathsize 14px style CO equals square root of 8 squared minus left parenthesis 16 over 3 right parenthesis squared end root CO equals square root of 64 minus 256 over 9 end root CO equals square root of fraction numerator 576 minus 256 over denominator 9 end fraction end root CO equals square root of 320 over 9 end root CO equals square root of fraction numerator 64 cross times 5 over denominator 9 end fraction end root CO equals 8 over 3 square root of 5 space text cm end text end style

Menghitung nilai sin A:

begin mathsize 14px style sin space straight A equals CO over AC sin space straight A equals fraction numerator begin display style 8 over 3 end style square root of 5 over denominator 8 end fraction sin space straight A equals 1 third square root of 5 end style



2. 
AB = √(AC² + BC² - 2 . AC . BC . cos C)
AB = √((2a)² + (2a√3)² - 2 . 2a . 2a√3 . cos 30°)
AB = √(4a² + 12a² - 8a²√3 . 1/2 √3)
AB = √(16a² - 12a²)
AB = √(4a²)
AB = 2a

3. 


4. 

5. luas ∆ = 1/2 × AC × BC × sin C




di

REMEDIAL PAT MTK WAJIB