LUAS SEGI-n BERATURAN
Dalam bangun datar segi n beraturan terdapat luas dan keliling yang dapat dihitung menggunakan jari jari dan sudut pusat. Sudut pusat ialah sudut yang terdapat pada segitiga dengan besar 360º/n. Dalam gambar di atas, kita dapat melihat tanda sudut berwarna merah yang menandakan sebagai letak sudut pusat. Sedangkan huruf x pada gambar tersebut menunjukkan sisi sisi pada bangun segi n beraturan. Pada kesempatan kali ini saya akan menjelaskan tentang rumus luas segi n beraturan, rumus keliling segi n beraturan, contoh soal luas segi n beraturan dan contoh soal keliling segi n beraturan. Untuk lebih jelasnya dapat anda simak di bawah ini.
Rumus Luas Segi (n) Beraturan Beserta Contoh Soal
Cara menghitung luas dan keliling bangun segi n beraturan memang menerapkan konsep luas segitiga yang menggunakan aturan sinus dan kosinus. Aturan sinus digunakan untuk menghitung luas segi n beraturan dan aturan kosinus digunakan untuk menghitung keliling segi n beraturan.
Apakah anda tahu bagaimana rumus luas bangun datar segi n beraturan itu? Bagaimana rumus keliling bangun datar segi n beraturan? Untuk menyelesaikan contoh soal luas segi n beraturan dan contoh soal keliling segi n beraturan tersebut dapat menggunakan rumus tertentu. Adapun rumus luas segi n beraturan dan rumus keliling segi n beraturan yaitu sebagai berikut:
Luas Bangun Segi n Beraturan
Seperti yang telah saya jelaskan di atas bahwa segi n beraturan dapat dihitung luasnya menggunakan konsep luas segitiga dengan sinus. Apabila dinyatakan dalam bentuk persamaan akan menjadi seperti di bawah ini:
Luas segitiga = ½ . r . r . sin θ = ½ r² sin 360°/n
Dari persamaan tersebut dapat diperoleh rumus luas segi n beraturan seperti berikut ini:
Luas segi n = n x Luas segitiga
Luas segi n = n/2 r² sin 360°/n
Keliling Bangun Segi n Beraturan
Untuk keliling bangun datar segi n beraturan dapat dihitung menggunakan konsep segitiga aturan kosinus, dimana sisi segi n (x) nya dapat ditentukan panjangnya. Adapun cara mencari panjang x pada segitiga menggunakan aturan kosinus yaitu:
Dari persamaan di atas dapat kita peroleh rumus keliling segi n beraturan seperti di bawah ini:
Catatan:
θ ialah sudut pusat yang besarnya 360º/n
Contoh Soal Segi n Beraturan
Setelah menjelaskan tentang rumus luas segi n beraturan dan rumus keliling segi n beraturan di atas. Selanjutnya saya akan membagikan contoh soal luas segi n beraturan dan contoh soal keliling segi n beraturan terkait rumus tersebut. Berikut contoh soal dan pembahasannya:
Tentukan luas segi 12 beraturan yang jari jari lingkaran luarnya memiliki panjang 9 cm?
Pembahasan.
Diketahui : r = 9 cm; n = 12
Ditanyakan : Luas = ?
Jawab :
Untuk menyelesaikan contoh soal tersebut dapat dilakukan dengan rumus seperti di bawah ini:
Luas = n/2 r² sin 360º/n
= 12/2 x 9² x sin 360º/12
= 6 x 81 x sin 30º
= 6 x 81 x ½
= 243 cm²
Jadi luas segi 12 beraturan tersebut ialah 243 cm².
JARI-JARI LINGKARAN LUAR DAN LINGKARAN DALAM SEGITIGA
Lingkaran Dalam Segitiga
Sebuah lingkaran berjari-jari r terdapat di dalam segitiga ABC yang panjang sisinya a, b, dan c. Diketahui bahawa setiap sisi segitiga menyinggung lingkaran sehingga terdapat tiga titik singgung. Antara segitiga dan lingkaran tersebut memiliki hubungan antara luas segitiga dan panjang jari-jari lingkaran. Ketiga sisi segitiga yang diketahui dapat digunakan untuk mengetahui besar luas segitiga atau kelilingnya. Dari luas tersebut kemudian dapat digunakan untuk mendapatkan panjag jari-jari lingkaran dalam segitiga.
Rumus jari-jari lingkaran dalam segitiga diberikan seperti persamaan di bawah.
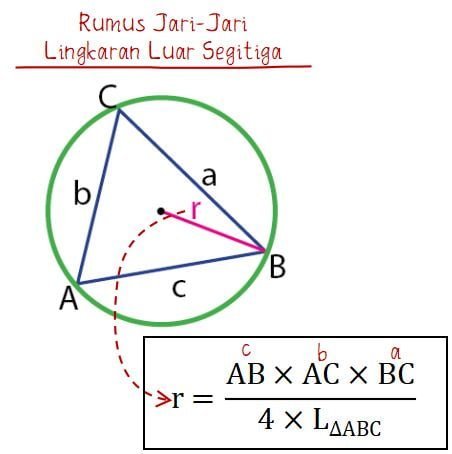
Lingkaran Luar Segitiga
Bentuk berikutnya adalah sebuah lingkaran berjari-jari r yang terdapat di luar segitiga ABC. Diketahui bahawa setiap sisi segitiga menyinggung lingkaran sehingga terdapat 3 titik singgung. Antara segitiga dan lingkaran tersebut memiliki hubungan antara luas segitiga dan panjang jari-jari lingkaran. luar segitiga.
Sisi-sisi segitiga ABC memiliki panjang sisi sama dengan a, b, dan c. Ketiga sisi segitiga yang diketahui dapat digunakan untuk mengetahui besar luas segitiga atau kelilingnya. Dari luas tersebut kemudian dapat digunakan untuk mendapatkan panjag jari-jari lingkaran dalam segitiga.
Jari-jari lingkaran tersebut dapat dihitung menggunakan rumus jari-jari lingkaran luar segitiga seperti persamaan di bawah.
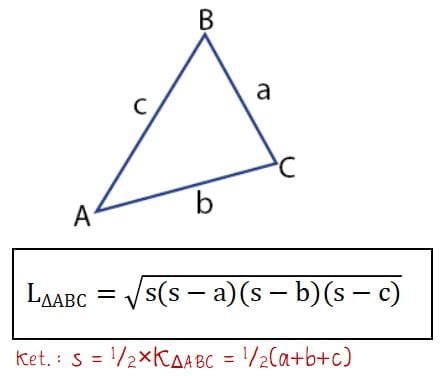
Luas Segitiga Beraturan dan Tidak Beraturan
Dua bahasan sebelumnya menyebutkan bahwa luas segitiga dibutuhkan dalam menghitung jari-jari lingkaran di dalam dan di luar lingkaran. Berdasarkan jenisnya, segitiga dibedakan menjadi dua yaitu segitiga berturan dan segitiga tidak berturan. Pada segitiga berturan, sisi alas dan tinggi segitiga dapat secara mudah dikenali. Sehingga, luas segitiga dapat dihitung menggunakan rumus umum bangun datar untuk menghitung luas segitiga.
Sedangkan pada segitiga tidak beraturan atau segitiga sembarang, bagian sisi dan alas segitiga tidak dapat ditentukan. Untuk menghihtung luas segitiga tak beraturan diperlukan rumus yang berbeda.
Kedua rumus segitiga yaitu segitiga beraturan dan tak beraturan diberikan seperti persamaan di bawah.
Luas Segitiga Beraturan
Luas Segitiga Tidak Beraturan
Contoh Soal Lingkaran Dalam dan Lingkaran Luar Segitiga (+Pembahasan)
Beberapan contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Lingkaran Dalam dan Lingkaran Luar Segitiga
Perhatikan gambar di bawah!

Jika panjang AC dan BC berturut-turut 8 cm dan 15 cm maka panjang jari-jari lingkaran dalam segitiga adalah ….
A. 5 cm
B. 3,5 cm
C. 3 cm
D. 2,5 cm
Pembahasan:
Gambar pada soal merupakan lingkaran dalam segitiga. Untuk mengetahui besar jari-jari dari lingkaran tersebut digunakan rumus jari-jari lingkaran dalam segitiga. Sebelumnya, kita perlu mencari sisi miring AB, keliling segitiga ABC, nilai s, dan luas segitiga ABC terlebih dahulu.
Menghitung sisi miring AC:
AB2 = AC2 + BC2
= 82 + 152
= 64 + 225
AB2 = 289
AB = √289 = 17 cm
Menghitung keliling segitiga ABC:
KΔABC = AB + AC + BC
KΔABC = 17 + 8 + 15 = 40 cm
Mencari nilai nilai s:
s = 1/2 × KΔABC
s = 1/2 × 40 = 20 cm
Mencari luas segitiga ABC:
LΔABC = 1/2 × AC × BC
LΔABC = 1/2 × 8 × 15 = 60 cm2
Jadi, panjang jari-jari lingkaran dalam segitiga tersebut sama dengan r = LΔABC/s= 60/20 = 3 cm.
Jawaban: C
Contoh 2 – Soal Lingkaran Dalam dan Lingkaran Luar Segitiga
Perhatikan gambar berikut!

Luas lingkaran di atas adalah ….
A. 10151/224 cm2
B. 10051/224 cm2
C. 10151/244 cm2
D. 10051/244 cm2
Pembahasan:
Untuk mengetahui luas daerah yang diarsir, kita perlu mencari jari-jari lingkaran terlebih dahulu. Sebelumnya, kita juga perlu mencari Keliling segitiga ABC, nilai s, dan segitiga ABC terlebih dahulu.

Menghitung keliling ΔABC:
KΔABC = AB + BC + CA
KΔABC = 21 + 10 + 17 = 48 cm
Menghitung nilai s:
s = 1/2 × KΔABC
s = 1/2 × 48 = 24 cm
Karena segitiga di luar lingkaran merupakan segitiga tidak beraturan, maka luas diperoleh dengan cara berikut.

Menghitung nilai jari-jari lingkaran:
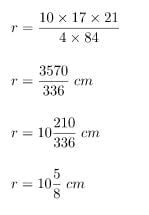
Menghitung luas lingkaran:
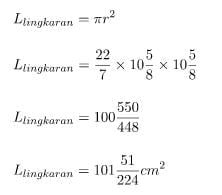
Jadi, luas lingkaran di atas adalah 10151/224 cm2
Jawaban: A
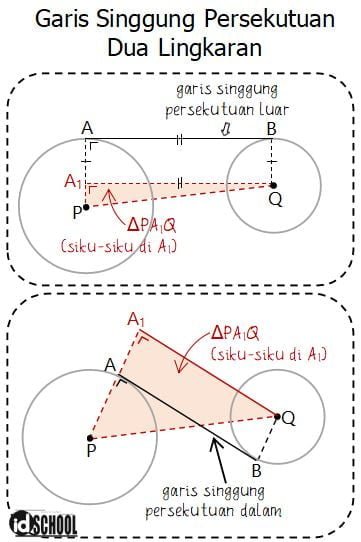
GARIS SINGGUNG PERSEKUTUAN LUAR/DALAM LINGKARAN
Ada dua jenis garis singgung lingkaran pada persekutuan dua lingkaran yaitu garis singgung persekutuan luar dan dalam pada dua buah lingkaran. Panjang garis singgung persekutuan dua lingkaran pada dua jenis tersebut dapat dihitung dengan rumus pythagoras. Di mana diketahui pada rumus pythagoras menyatakan hubungan ketiga sisi pada segitiga siku-siku.
Pada segitiga siku-siku terdapat dua buah sisi tegak dan satu buah sisi miring. Garis singgung persekutuan dua lingkaran merupakan salah satu sisi tegak pada segitiga siku-siku. Sedangkan panjang jumlah/selisih jari-jari menjadi sisi tegak yang satunya. Sisi miring segitiga merupakan panjang garis singgung lingkaran pada persekutuan dua lingkaran. Tiga buah ruas garis yang merupakan panjang garis singgung, jarak dua pusat dua lingkaran, dan jumlah/selisih segitiga membentuk sebuah segitiga. Antara garis singgung persekutuan dua lingkaran dan garis jumlah/selisih jari-jari lingkaran selalu membentuk sudut siku-siku. Sehingga terbentuklah sebuah segitiga siku-siku yang hubungan ketiga sisinya sesuai dengan rumus pythagoras.
Garis Singgung Persekutuan Luar Dua Lingkaran
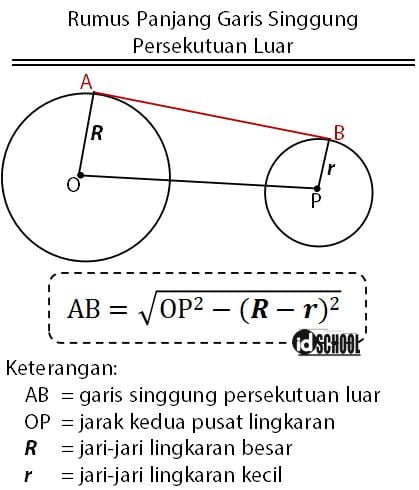
Dua buah lingkaran yang berpusat pada titik O dan P memiliki panjang jari-jari yang berbeda. Panjang jari-jari lingkaran dengan pusat O adalah R, sedangkan panjang jari-jari lingkaran dengan pusat P adalah r. Jarak kedua pusat pada dua lingkaran tersebut adalah OP. Terdapat sebuag garis yang menyinggung kedua lingkaran yaitu garis AB.
Gambar di bawah menunjukkan letak garis AB yang merupakan garis singgung lingkaran pada persekutuan luar dari dua lingkaran.
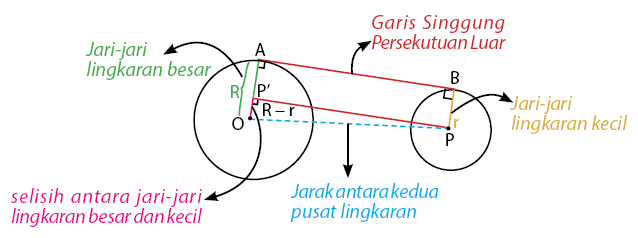
Garis AB adalah garis singgung lingkaran pada persekutuan luar dua lingkaran. Perhatikan bahwa panjang AB sama dengan panjang PP’. Sehingga dengan menghitung panjang PP’ secara otomatis dapat mengetahui panjang ruas garis AB. Di mana, garis AB merupakan garis singgung persekutuan luar dua lingkaran.
Segitiga PP’O merupakan segitiga siku-siku yang siku-siku di P’. Hubungan ketiga sisi pada segitiga siku-siku memenuhi persamaan pada rumus Pythagoras. Sehingga dapat diperoleh persamaan P’P2 = OP2 ‒ P’O2 dengan P’O = OA ‒ BP = R ‒ r. Atau persamaan dapat juga dibentuk dalam bentuk P’P2 = OP2 ‒ (R ‒ r)2.
Dengan demikian panjang garis singgung lingkaran pada persekutuan luar pada dua lingkaran dapat diperoleh melalui rumus garis singgung persekutuan luar berikut.
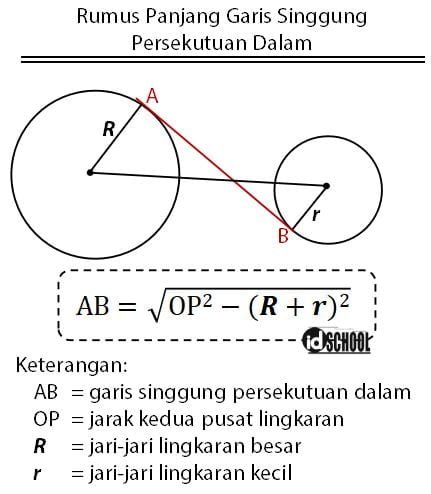
Garis Singgung Persekutuan Dalam Dua Lingkaran
Garis singgung persekutuan dalam dua lingkaran juga melibatkan dua buah lingkaran dan sebuah garis singgung, sama seperti pada garis singgung persekutuan luar. Bedanya terletak pada posisi garis singgung lingkaran. Dua titik pada garis singgung persekutuan luar dua lingkaran terletak di sisi yang sama. Sedangkan pada garis singggung persekutuan dalam, dua titik singgung terletak pada sisi yang bersebrangan.
Gambar di bawah menunjukkan posisi garis singgung lingkaran pada persekutuan dalam yang menyinggung dua buah lingkaran.
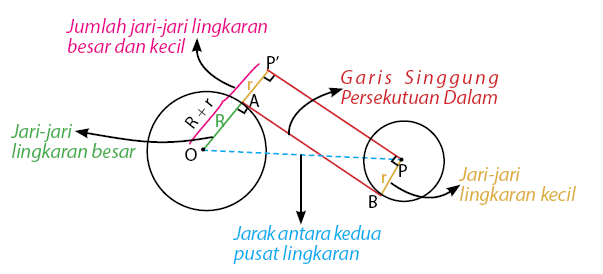
Perhatikan bahwa segitiga PP’O merupakan segitiga siku-siku yang siku-siku di P’. Hubungan antara P’O, P’P, dan OP dapat sesuai pada rumus Pythagoras yaitu P’P2 = OP2‒ P’O2. Karena PO’ = OA + BP = R + r maka bentuk persamaan dapat juga dinyatakan dalam P’P2 = OP2‒ (R + r)2
Sehingga, rumus garis singgung persekutuan dalam dua lingkaran dapat dinyatakan dalam rumus di bawah.
Contoh Soal Garis Singgung Persekutuan Dua Lingkaran dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman terkait bahasan di atas. Setiap soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Garis Singgung Persekutuan Luar Dua Lingkaran
Dua buah lingkaran memiliki panjang garis singgung persekutuan luar 24 cm dan jarak kedua titik pusat lingkaran 26 cm. Jika panjang jari-jari lingkaran besar 18 cm, maka panjang jari-jari lingkaran yang lain adalah ….
A. 6 cm
B. 8 cm
C. 9 cm
D. 10 cm
Pembahasan:
Berdasarkan data pada soal, kita dapat peroleh gambar di bawah.

Diketahui bahawa,
- Garis singgung persekutuan luar dua lingkaran: AB = 24 cm
- Jarak keuda pusat lingkaran: OP = 26 cm
- Panjang jari-jari lingkaran besar: OA = 18 cm
- Panjang jari-jari lingkaran kecil: OB = r
Menghitung panjang garis singgung AB:
AB2 = OP2 ‒ (OA ‒ r)2
242 = 262 ‒ (18 ‒ r)2
676 = 576 ‒ ( 18 ‒ r)2
(18 ‒ r)2 = 676 ‒ 576
(18 ‒ r)2 = 100
18 ‒ r = 10
‒r = 10 ‒ 18
‒r = ‒8 → r = 8 cm
Jadi, panjang jari-jari lingkaran yang lain adalah 8 cm.
Jawaban: D
Contoh 2 – Soal Garis Singgung Persekutuan Dua Lingkaran
Perhatikan gambar berikut!

Panjang jari-jari lingkaran besar dan kecil berturut-turut adalah 10 cm dan 5 cm. Jarak kedua pusat lingkaran adalah 25 cm. Panjang garis singgung AB adalah ….
A. 12 cm
B. 15 cm
C. 17 cm
D. 20 cm
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.
- Panjang jari-jari lingkaran besar: R = 10 cm
- Panjang jari-jari lingkaran kecil: r = 5 cm
- Jarak kedua pusat lingkaran: OP = 25 cm
Menghutng panjang garis singgung AB:
AB2 = OP2 ‒ PC2
AB2 = OP2 ‒ ( R + r )2
= 252 ‒ ( 10 + 5)2
= 625 ‒ 225
AB2 = 400
AB = √400 = 20 cm
Jadi, panjang garis singgung AB adalah 20 cm.
Jawaban: D
Daftar Pustaka:
1. http://www.antotunggal.com/2021/10/contoh-rumus-luas-segi-n.html
2. https://idschool.net/smp/lingkaran-dalam-dan-lingkaran-luar-segitiga/
3. https://idschool.net/smp/garis-singgung-lingkaran/




.png)